La meccanica quantistica (in seguito MQ) è la teoria della meccanica attualmente più completa, in grado di descrivere il comportamento della materia, della radiazione e le reciproche interazioni, dove le precedenti teorie classiche risultano inadeguate; le misure da essa calcolate sono estremamente precise e non sbagliano mai, il problema è che non si capisce il perché, come possa funzionare.
Capire la MQ non è possibile, il suo essere non rientra nella sfera dei nostri concetti naturali e tantomeno nel nostro linguaggio; Ludwig Wittgenstein, filosofo, ingegnere e logico austriaco, considerato da alcuni il massimo pensatore del XX secolo, ha fatto questa interessante osservazione:
‘E’ il linguaggio a doversi adattare ai fatti e non l’inverso. Cercare di modellare l’interpretazione di un fenomeno su un linguaggio già formato e riempito a priori può solo condurre a false conclusioni sulla natura delle cose’.
A voler fare filosofia è come aver fede in Dio, si afferma che Dio esiste, vediamo e godiamo del suo creato, ma non capiamo i suoi piani ed il suo modo di operare; l’americano Richard Feynman, Nobel per la fisica nel 1965 per l’elaborazione dell’elettrodinamica quantistica, disse: ’Penso di poter affermare che nessuno capisce la MQ”.
E’ importante specificare che la M.Q. risulta valida per qualsiasi corpo, ma assume significato nei fenomeni caratteristici della scala di lunghezza o di energia atomica e subatomica, comparabili con la ‘Costante di Plank’, il cui valore è circa 6,626 · 10 -34 J · s (Joule per secondo); più precisamente la MQ è lo strumento che descrive fenomeni di cui misuriamo alcune proprietà, ma che non riusciamo a vedere nei dettagli, non riusciamo neanche ad immaginarli, sono parte intrinseca della natura e il loro limite è la costante di Plank.
Nel mondo macroscopico, quindi, non si riescono a percepire, un po’ come indicato da Einstein con la ‘Relatività ristretta’, dove si ha un aumento della massa all’aumentare della sua velocità, ma questo fenomeno lo possiamo osservare solo all’approssimarsi della velocità della luce.
Proprio questa analogia fu fonte di discussione tra Heisenberg ed Einstein; quando quest’ultimo criticava le logiche che avevano portato Heisenberg, neanche ventisettenne, alla formulazione del principio di indeterminazione, questo gli fece notare che anche Einstein aveva adottato una logica analoga, affermando l’esistenza di un limite che la velocità non può superare, in contrapposizione con la consolidata ‘composizione delle velocità’ galileiana.
Per spiegare la MQ, o meglio per poterne parlare, vediamo quali sono le sue caratteristiche; cechiamo di approfondire tre suoi principi fondamentali:
- Principio di Complementarietà
Ogni particella ha una doppia natura, un comportamento diverso a seconda della situazione, ondulatoria o corpuscolare, cioè può essere identificata come un corpo materiale o come un’onda.
Per esempio la luce si definisce un’onda elettromagnetica e si comporta come tale, nei fenomeni della diffrazione, dell’interferenza e così via, mentre nei fenomeni fotoelettrici, si comporta come un corpuscolo. Quindi le particelle sono Onde o Corpuscoli? Ne’ l’uno e né l’altro.
Come possiamo capire questa anomalia che sembra essere illogica; alla fine del 1700 si conoscevano due classi animali: Mammiferi e Ovipari. Quando si individuò l’Ornitorinco ci fu un po’ di confusione, chi lo definiva Mammifero rifiutava che deponesse le uova, altri lo vollero Oviparo rifiutando che avesse le mammelle e che secernesse il latte. Eppure l’Ornitorinco, se pur ‘anomalo’ esisteva, ma la sua anomalia non dipendeva da lui, ma solo dal fatto che lo si voleva incastrare in una delle due possibili Classi animali che si conoscevano allora; occorreva creare la nuova classe degli Ovovivipari.
Quindi, in conclusione, gli oggetti che considera la MQ trascendono la classificazione tradizionale, ma sono perfettamente spiegabili da un impianto matematico estremamente complesso che, come già detto, descrive perfettamente tutti i fenomeni che osserviamo, pur non capendo il suo profondo significato.
- Principio di Indeterminazione
E’ impossibile guardare (misurare) qualcosa e vederlo come è realmente, ma solo come è nel momento in cui lo si vede (misura). Un esempio banale e ovviamente non corretto, ma che può rendere una vaga idea del concetto, può essere la situazione di un uomo in una stanza al buio che cerca il suo gatto; l’uomo si muove all’interno della stanza finché calpesta la coda del gatto, cioè lo trova, ma proprio nello stesso istante il gatto è scappato via, quindi la determinazione della posizione del gatto avviene solo nell’istante del ritrovamento (misura), non ha un suo unico valore a priori, ma infinite possibilità; non conosco la posizione del gatto ne prima ne dopo che gli ho calpestato la coda!
- Principio di Sovrapposizione degli stati
La logica conseguenza del precedente principio è che lo ‘Stato di un’osservabile’ di un sistema fisico (il gatto nella stanza) risulta essere la somma delle probabilità di trovarsi in uno dei suoi possibili ‘Stati‘.
Per la MQ il gatto si trova ovunque nella stanza prima e dopo il suo ritrovamento, con una certa possibilità di trovarsi in un determinato punto; questa è una proprietà intrinseca, non perché non abbiamo i mezzi per poterla misurare, anche se non si riesce a capire!
Qualcuno potrebbe affermare che comunque, anche se l’uomo non sa dov’è il gatto, quest’ultimo si trovi in una determinata posizione in un certo istante! Proprio questa affermazione aveva dato origine alla disputa di Einstein con Heisenberg, ed è il cosiddetto ‘realismo di Einstein’ a cui piaceva dire:
‘la Luna è lassù anche quando nessuno la sta osservando’; ma questo è un limite della nostra mente, riferito al nostro mondo macroscopico ed al linguaggio che usiamo.
Un esempio che può aiutare a capire la definizione degli ‘Stati’ è quello di un uomo che lancia una moneta e la fa cadere al suolo, ma la moneta finisce sotto la poltrona. Ora la moneta si può trovare in tre situazioni (Stati): Testa, Croce o in verticale. Finché l’uomo non la vede, lo stato della moneta è la somma delle probabilità che la moneta si in uno dei suoi possibili tre stati.
Solo quando l’uomo sposta la poltrona e la vede (misura) allora i tre possibili stati ‘collassano’ in uno di essi ed in modo ‘INTRINSECAMENTE CASUALE’.
Sembra quindi che l’azione di osservare la realtà ne determini una mutazione, da sovrapposizione dei possibili stati ad uno specifico e in modo casuale! Questo è sconvolgente, sembra assurdo, non si riesce a capire!
In conclusione, la MQ non dice come è la realtà, ma ci consente, tramite il suo formalismo matematico, di spiegare i vari fenomeni che osserviamo e solo tramite esso è possibile dare delle definizioni.
Una particella non è ne corpuscolo ne onda, ma è rappresentabile tramite una ‘funzione d’onda’, cioè una funzione matematica definita in uno spazio (spazio di Hilbert) di numeri complessi. La formula che associa lo stato di una particella alla sua funzione d’onda è data dall’equazione di Schrödinger, cioè un’equazione differenziale parziale lineare che descrive l’evoluzione di uno stato quantico in un modo simile alle leggi di Newton (la seconda legge in particolare) nella meccanica classica.
Da un punto di vista fisico quindi, possiamo immaginarci la particella come una densità di energia che ha una probabilità di trovarsi da qualche parte nello spazio e questa probabilità è estraibile dall’onda associata alla particella.
Ma se ci poniamo la questione della realtà fisica che c’è dietro non ne sappiamo nulla e forse non ne sapremo mai nulla perché è qualcosa che per sua natura ci sfugge.
Immaginiamo che un regista voglia rappresentare l’idea di un viaggio; potrebbe riprendere un treno che parte, oppure l’immagine di un passeggero che guarda il paesaggio scorrere dal finestrino, oppure delle valigie alla stazione degli autobus; tutte sono valide e nessuna, assumono una loro valenza a seconda del contesto in cui vengono inserite, ma se noi andiamo alla ricerca di un qualcosa di reale e fisico che descriva il viaggio in modo preciso ed inequivocabile allora ci dobbiamo rassegnare, stiamo cercando qualcosa che non possiamo trovare, ma non perché non siamo in grado di capirlo o perché non esista o per dei limiti della nostra capacità di ricerca, ma perché il concetto di viaggio, per sua natura non può essere imbrigliato.
Per chi volesse approfondire la questione matematica a seguire darò un brevissimo accenno sui numeri complessi e sulla lunghezza d’onda.
NUMERI COMPLESSI
Abbiamo detto che la MQ non si può esprimere con numeri reali, ma solo con numeri complessi (equazione di Schrödinger), da qui l’impossibilità di raccontarla con il linguaggio naturale.
I numeri complessi sono formati da numeri reali e da numeri immaginari; quest’ultimi hanno lo scopo di poter calcolare la radice quadrata di un numero negativo, la cui specifica parte dalla definizione di un’unità immaginaria identificata con la lettera ‘i‘ che rappresenta la radice di -1, quindi si ha questa definizione:
i = -1 da cui i 2 = -1
quindi per risolvere la radice di -4 possiamo esprimere:
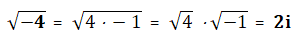
Più precisamente, i numeri complessi sono la somma algebrica di numeri reali ed immaginari, per cui li possiamo definire come una coppia di numeri, il primo che identifica la parte reale ed il secondo la parte immaginaria; il formalismo è quello di indicare la coppia separata da una virgola e racchiusa tra parentesi tonde: (R,i). Per poterli rappresentare geometricamente quindi non è sufficiente una retta (come per i numeri reali), ma occorre utilizzare un piano con l’asse orizzontale che rappresenta la retta dei numeri reali e l’asse verticale che rappresenta la retta dei numeri immaginari.
Per esempio i numeri complessi (-0.8,i/2), (1, i), (2,i), (3,i), (-2,-i) e (3,-i) si rappresentano così:
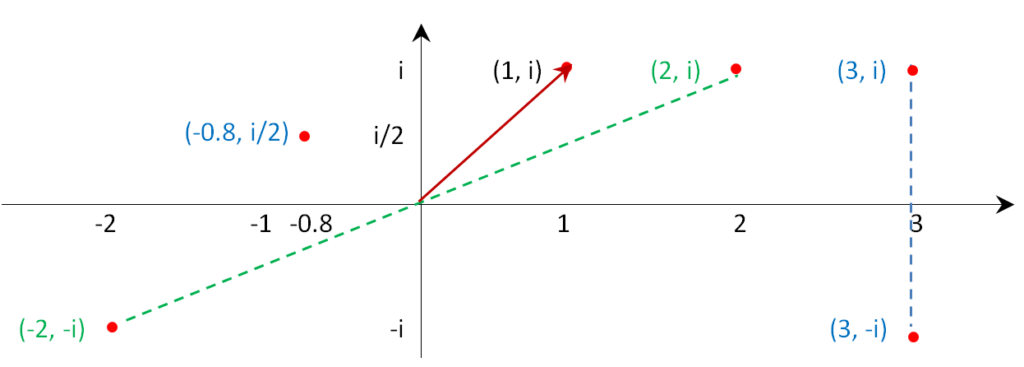
Cioè un numero complesso può essere rappresentato come un vettore nel piano di Argand-Gauss.
Loro proprietà: Elemento neutro, opposto, coniugato ed inverso o reciproco
Nell’insieme dei numeri reali sappiamo che 0 e 1 sono gli elementi neutri rispetto alla somma ed al prodotto e che, se R è un numero reale diverso da zero, –R è il suo opposto e 1/R = R -1 è il suo inverso.
Anche nell’insieme dei numeri complessi possiamo definire tali quantità. In particolare:
(0,0) è l’elemento neutro rispetto alla somma; graficamente coincide con l’origine degli assi del piano complesso;
(-a,-b) è l’opposto del numero complesso (a,b); graficamente l’opposto di un numero complesso è il simmetrico rispetto all’origine degli assi, nell’esempio (2,i) ed il suo opposto (-2,-i) .
(1,0) è l’elemento neutro rispetto al prodotto.
(a,-b) è il coniugato del numero complesso (a,b). In dettaglio, dato il numero complesso z = (a,b) si indica il suo complesso coniugato con
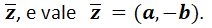
Da un punto di vista grafico il coniugato di un numero complesso è il suo simmetrico rispetto all’asse dei numeri reali, nell’esempio (3,i) ed il suo coniugato (3,-i).
Non espongo l’inverso moltiplicativo perché è un po’ complicato e non ci serve allo scopo.
Nel momento in cui, tramite la MQ, misuriamo la posizione di un oggetto facciamo un’operazione matematica, e precisamente moltiplichiamo il numero complesso misurato per il suo complesso coniugato e lo eleviamo al quadrato ottenendo il vettore che definisce la probabilità della posizione del punto rispetto l’origine degli assi, questo fa rientrare la funzione di numeri immaginari in numeri reali, cioè facciamo collassare lo stato da uno spazio immaginario in uno reale e quindi riusciamo a misurarlo e a darne una spiegazione umana.




Lascia un commento
Devi essere connesso per inviare un commento.