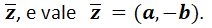DIFFERENZE TRA MECCANICA CLASSICA E MECCANICA QUANTISTICA.
Banalmente la prima si basa su formalismi e concetti che presuppongono misure ‘continue’, cioè piccole a piacere, la seconda invece, come dice lo stesso nome, su misure ‘discrete’, asserisce, cioè, che ci sono misurazioni al disotto delle quali non si può scendere, ma ATTENZIONE, non per l’incapacità di poterle misurare, ma per loro ‘natura intrinseca’.
La ‘Relatività Ristretta’ di Einstein si basa sull’assunzione che ci sia una costante valida per ogni osservatore, cioè la ‘Velocità della luce’, indicata normalmente con la lettera c il cui valore, nel vuoto, è circa 3 · 10 8 m/s
La meccanica quantistica si basa, anch’essa, sull’asserzione che ci sia una costante, la cosiddetta ‘Costante di Plank’, indicata con la lettera h il cui valore è circa 6,626 · 10 -34 J · s (Joule per secondo).
Ora vediamo di capire cos’è e quali implicazioni comporta.
CONSIDERAZIONI SUL MODO DI OPERARE
Prima di entrare nel merito, vorrei anticipare due modalità operative nello studio della Fisica che vengono utilizzati nei formalismi matematici, praticamente sempre; questo perché risulta più comodo o utile.
La prima modalità sfrutta le ‘Proprietà fondamentali delle uguaglianze numeriche’
1) Sommando o sottraendo uno stesso valore ad entrambi i membri dell’uguaglianza il valore dell’uguaglianza non cambia.
2) Moltiplicando o dividendo entrambi i membri di un’uguaglianza per uno stesso valore diverso da 0 il valore dell’uguaglianza non cambia
Questo concetto si può estendere dai valori numerici anche alle dimensioni delle grandezze.
Ricordiamo cosa significa ‘dimensione’ di una grandezza; indica le unità di misura delle grandezze fondamentali che la costituiscono.
Per es.: la dimensione della velocità è una lunghezza diviso un tempo [V]=[L]/[T]
la dimensione dell’accelerazione è una lunghezza diviso un tempo al quadrato [A]=[L]/[T]2
la dimensione dell’Energia è una massa per la velocità al quadrato [m]·[V2] cioè [m]·[L]2/[T]2
La seconda, partendo da una formula, utilizzare unità di misura differenti per una variabile, oltre che per comodità anche per essere più coerenti con quello che si osserva.
Questo modo di operare, che utilizzeremo inseguito, mi lasciò alquanto perplesso quando frequentavo i primi anni dell’Università di Fisica a Genova, facendomi nascere delle perplessità e dubbi, non esplicitamente definiti, ma istintivi e, forse per questo motivo, tenute in disparte, procedendo con la frase ‘mi fido’ (ma rimane un punto da chiarire).
FONDAMENTI DI CINEMATICA
Cominciamo dai concetti base di movimento di un corpo; i parametri con cui lo possiamo esprimere sono la sua ‘Massa’, ‘Posizione’, ‘Velocità’, ‘Accelerazione’.
A scuola ci viene insegnato un metodo visivo per esporre questi concetti tramite un grafico, detto anche ‘Grafico orario’ perché è una funzione del Tempo.
Per descrivere la velocità (variabile v espressa in metri al secondo) di un corpo si può disegnare la funzione dello spazio (variabile x espressa in metri) che percorre al variare del tempo (variabile t espressa in secondi).
Per esempio un corpo fermo a 7 m. dallo 0 si può esprimere tramite questa funzione:
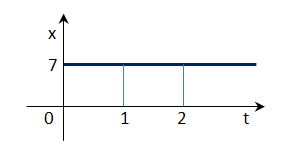
Cioè, in qualsiasi momento si trova sempre a 7 m dallo 0, sia all’inizio, dopo un secondo, dopo 2 e così via
In questo caso del corpo fermo, cioè velocità = 0, si vede che la pendenza è zero.
Analogamente un corpo che si muove a velocità costante lo possiamo rappresentare tramite una semiretta che ha una pendenza costante che indica il valore della velocità stessa.
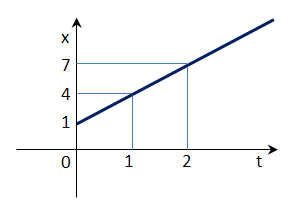
1 m dallo 0 quando iniziamo la misura,
4 m dopo 1 secondo, 7 m dopo 2 secondi, … cioè un incremento costante dello spazio nel tempo di 3 metri ogni secondo. Possiamo dire che si muove alla velocità di 3 metri al secondo.
Nessuno però ci vieta, anzi, nel linguaggio comune è più usato, rappresentare la velocità in funzione dello spazio, quindi non più un grafico ‘orario’.
Rappresentiamo il nuovo grafico della velocità costante; in ogni punto ha sempre lo stesso valore:
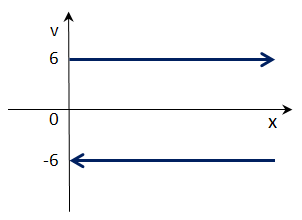
Possiamo dare anche un verso alla velocità, ponendo la convenzione che sia:
positiva da sinistra a destra ( +6 ) si allontana negativa da destra a sinistra ( -6 ) si avvicina
MOTI PERIODICI
Quello che abbiamo visto ci è servito per capire gli strumenti che verranno utilizzati.
Ma il moto rettilineo uniforme non è un moto realistico, in natura si trovano movimenti circoscritti in uno spazio limitato: un pianeta attorno al Sole, una molecola in un contenitore, un elettrone attorno al protone nell’atomo di Idrogeno e così via.
Questi sono movimenti VINCOLATI, essendo limitati nello spazio, e quindi gli si può associare una ripetitività nel tempo, cioè si dicono PERIODICI; il tempo di rotazione della Terra, quanto ci mette la molecola a sbattere tra una parete e l’altra, il tempo di rotazione del Neutrone, …
Vediamo allora l’esempio di una pallina che rimbalza in modo perfettamente elastico tra due pareti, riproducibile sperimentalmente con una molecola in un contenitore.
Consideriamo la velocità in funzione dello spazio del moto della molecola in un contenitore; prendendo come origine degli assi il centro del contenitore; avremo la parete sinistra alla lunghezza -L dal centro, la parete destra a +L, la velocità della molecola positiva +V, quando si muove dalla parete di sinistra a quella di destra, e negativa -V quando torna indietro; al momento iniziale la molecola si trova al centro del contenitore, quindi x = 0 e si muove da sinistra a destra quindi, per nostra convenzione, con velocità +v, raggiunge la parete destra x = +L (Fase 1), rimbalza in modo elastico, quindi la velocità si inverte (ipotizziamo in un tempo infinitesimo, o perlomeno insignificante per il nostro esempio) diventando negativa -v, la molecola allora raggiunge la parete di sinistra x = -L (Fase 2), si invertono le condizioni e si ritorna allo stato iniziale al punto x = 0 (Fase 3) completando il ciclo per continuare in modo identico, ripetendosi nel tempo.
Ecco il primo esempio anticipato nel paragrafo ’Considerazioni sul modo di operare‘ dove abbiamo detto che a volte conviene cambiare le dimensioni di una variabile, perciò, anziché utilizzare la velocità come variabile, possiamo moltiplicarla per la massa della molecola. Questa nuova unità di misura (velocità · massa) non è altro che la quantità di moto rappresentata dal simbolo P.
Questa unità di misura, per ragioni storiche, è molto utilizzata in ‘Meccanica Razionale’ ed aggiunge una grandezza che consente di generalizzare la formula, da un punto geometrico ad un corpo di massa generica.
Quindi il grafico della quantità di moto in funzione dello spazio, formalmente P(x), sarà:
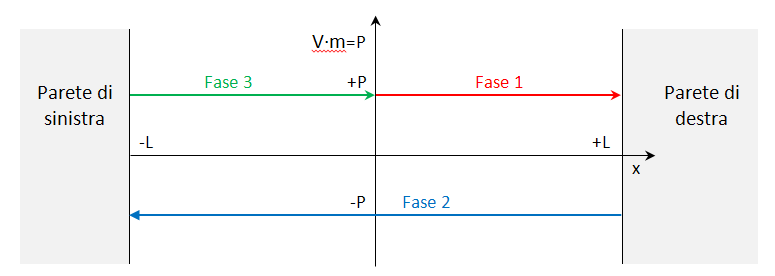
Con questo grafico abbiamo disegnato la traiettoria di un punto libero nello ‘Spazio delle Fasi’, argomento del terzo anno di Fisica teorica!
Il moto periodico in uno spazio unidimensionale, come nell’esempio, è descritto quindi, nello Spazio delle Fasi, da una traiettoria chiusa.
Se dovessimo rappresentarlo nello spazio tridimensionale occorrerebbe un grafico a 6 dimensioni, 3 per specificare la x e 3 per la P, ovviamente molto più complesso nel formalismo, ma concettualmente perfettamente uguale.
Ora noi possiamo definire una nuova unità di misura che chiameremo AZIONE, il cui simbolo è J, e che rappresentata dall’area definita dalla traiettoria in quella figura. L’area del rettangolo è base per altezza, dove, in questo caso, la base è data da 2L, l’altezza da 2P. Quindi l’area sarà: J = 2P · 2L quindi: J = 4PL
La dimensione dell’AZIONE è data da una quantità di moto per una lunghezza, o anche una velocità per una massa per una lunghezza, V·m·L, scomponendo la velocità in spazio/tempo si ha: L/T·m·L ottenendo infine: m·L2/T e può essere espressa in Kilogrammi per metri al quadrato diviso secondi: Kg·m2/s
Per semplificare, come avevamo già anticipato, se moltiplichiamo numeratore e denominatore per il tempo T, avremo: T·m· L2/T2, siccome L2/T2 è una velocità al quadrato allora T·m·V2, ma abbiamo visto che m·V2 rappresenta un’energia quindi l’Azione si può esprimere come un’Energia per il tempo esprimibile in Joule per secondo: J = E·T La costante di Plank h è proprio un’ AZIONE
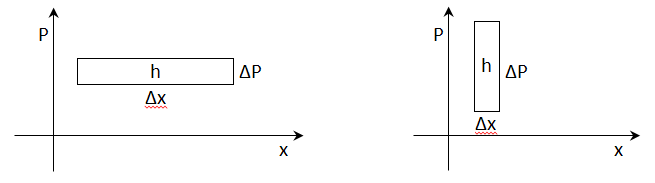
Il ‘Principio di indeterminazione di Heisenberg’ si basa sull’asserzione che un’Azione non possa essere più piccola del valore di h. Ne deriva che se prendiamo la superficie più piccola possibile, quindi con area h e stringiamo la base (x) in un intervallo Δx l’altezza (P) crescerà proporzionalmente ed analogamente se stringiamo l’altezza (P) in un intervallo ΔP la base (x) crescerà anch’essa proporzionalmente. Quindi più definisco la posizione del corpo, più ampia è l’incertezza del valore della sua quantità di moto o, che è concettualmente lo stesso, della sua velocità e viceversa.
La formula quindi diventa: Δx · ΔP ≥ h